Projects
A rather comprehensive list of projects that I have worked on, grouped by area of interest.
Learning, generalization, and domain adaptation
-
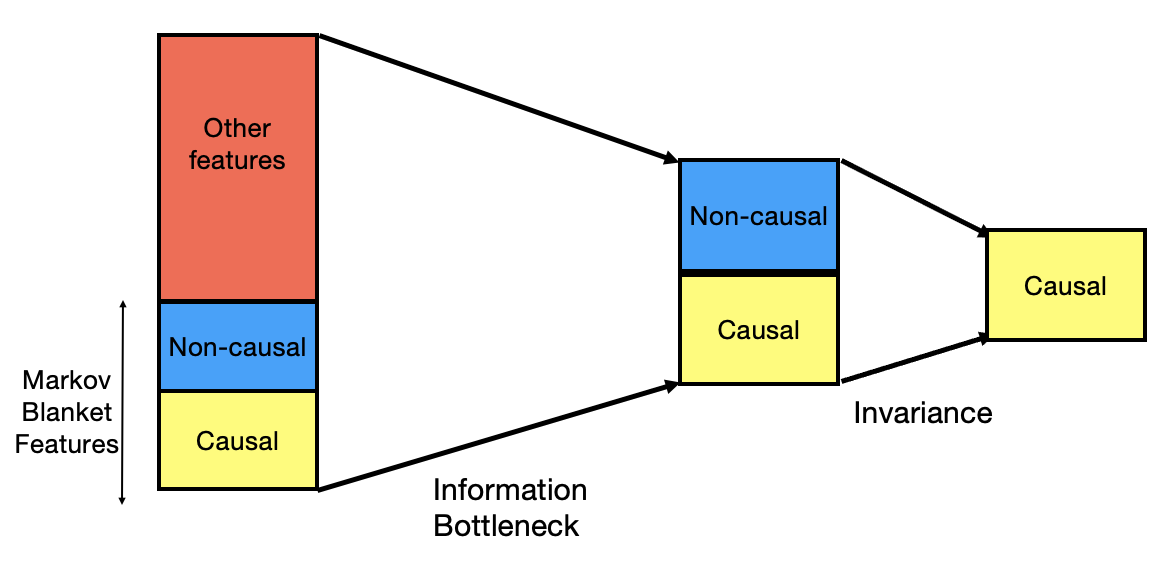Invariance Principle Meets Information Bottleneck for Out-of-Distribution Generalization We prove that using the "information bottleneck" along with invariance helps address key failures of IRM. We propose an approach that incorporates both of these principles and demonstrate its effectiveness.
Lead: Kartik Ahuja -
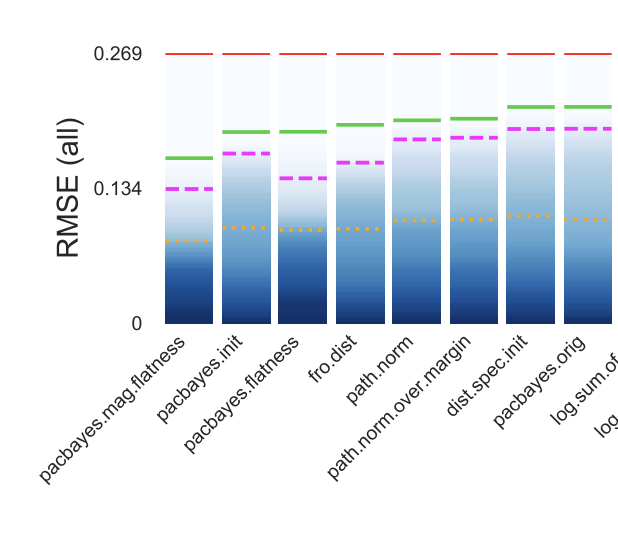In Search of Robust Measures of Generalization We look into the experimental evaluation of generalization measures for neural networks. We argue that generalization measures should be evaluated within the framework of distributional robustness and provide methodology and experimental results on a variety of architectures.
Lead: Karolina Dziugaite, Alexandre Drouin (ServiceNow/ElementAI) -
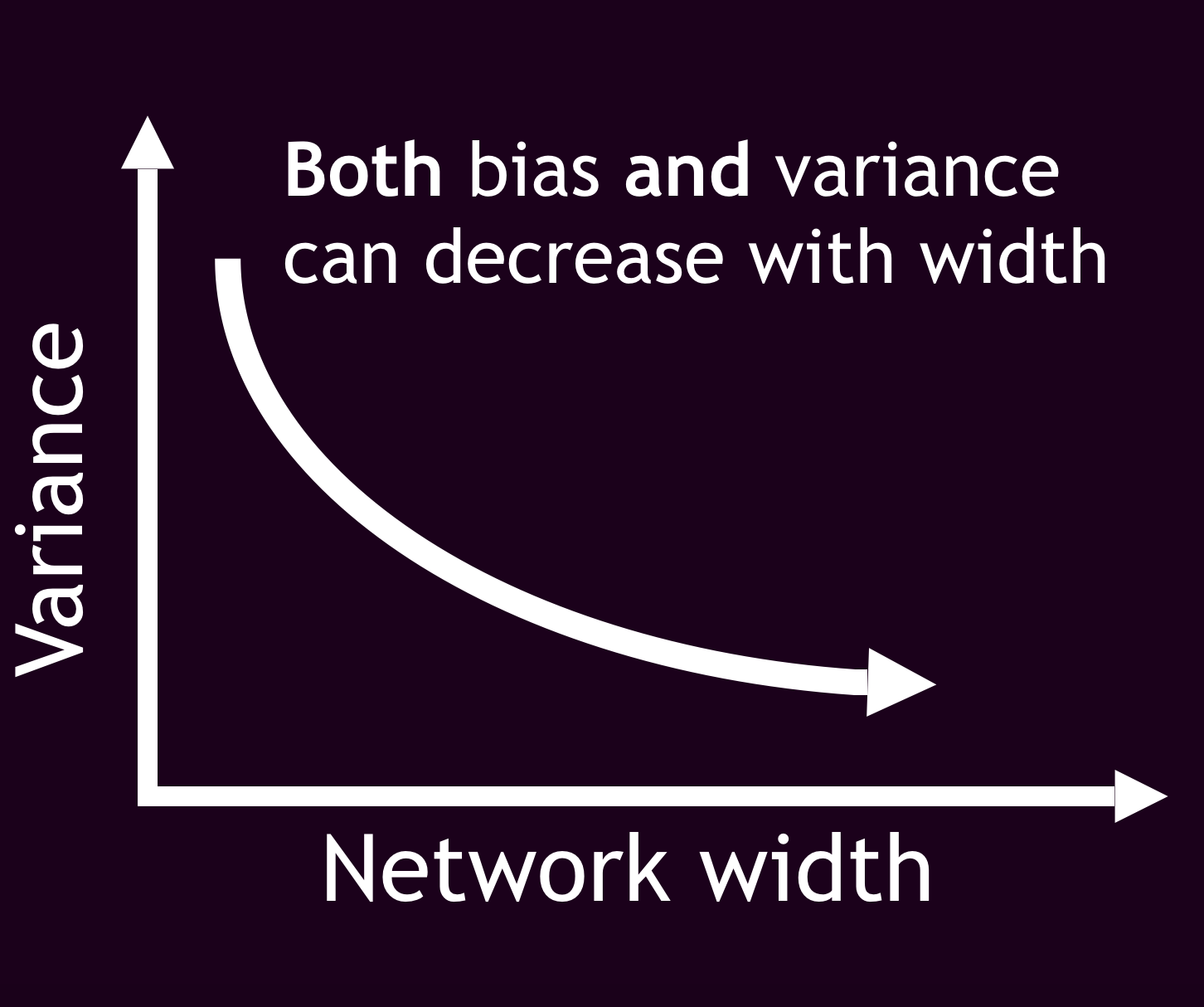A Modern Take on the Bias-Variance Tradeoff in Neural Networks We measure prediction bias and variance in NNs. Both bias and variance decrease as the number of parameters grows. We decompose variance into variance due to sampling and variance due to initialization.
Lead: Brady Neal -
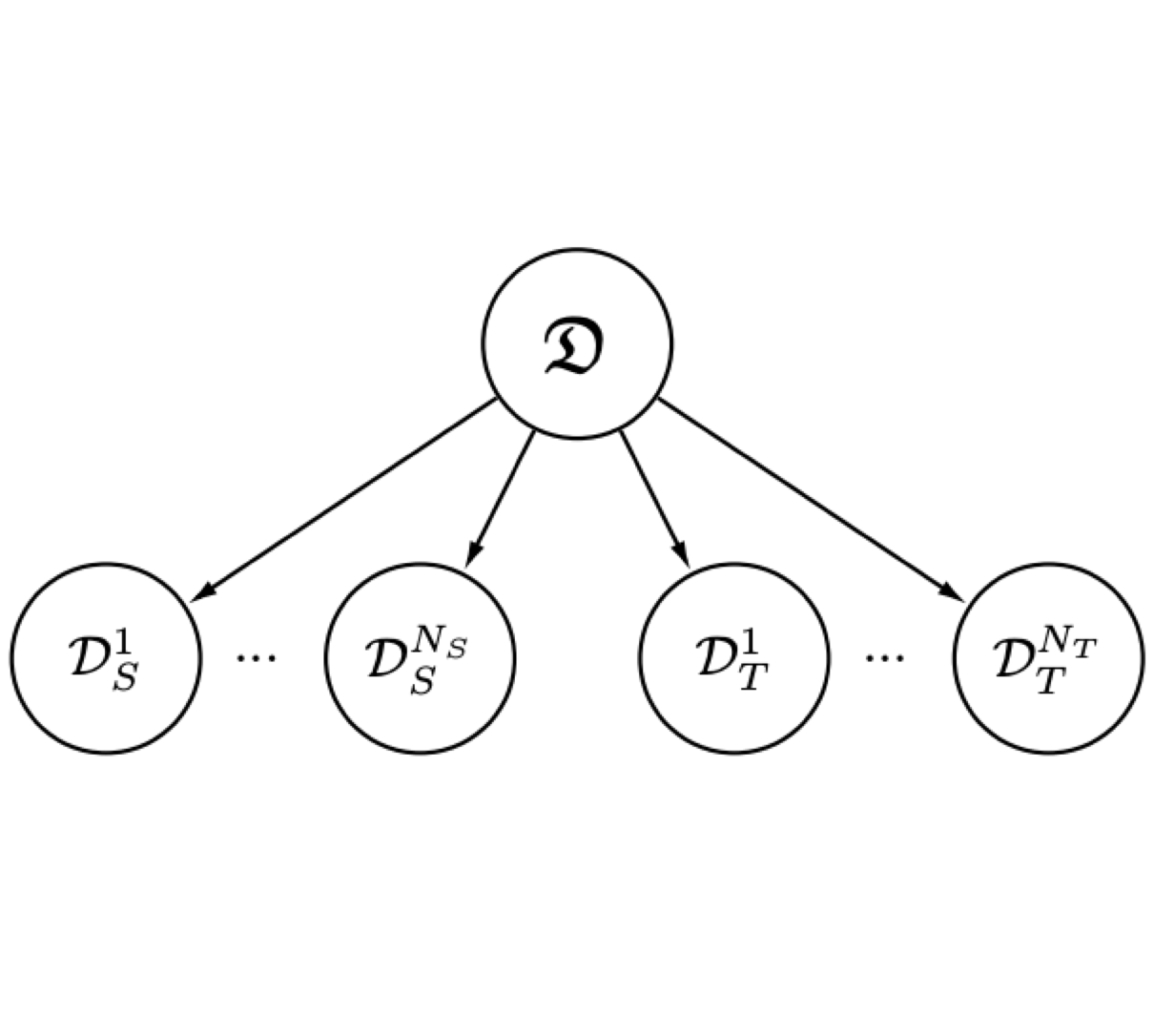Generalizing to unseen domains via distribution matching We propose a process that enforces pair-wise domain invariance while training a feature extractor over a diverse set of domains. We show that this process ensures invariance to any distribution that can be expressed as a mixture of the training domains.
Lead: Isabela Albuquerque, João Monteiro (INRS) -
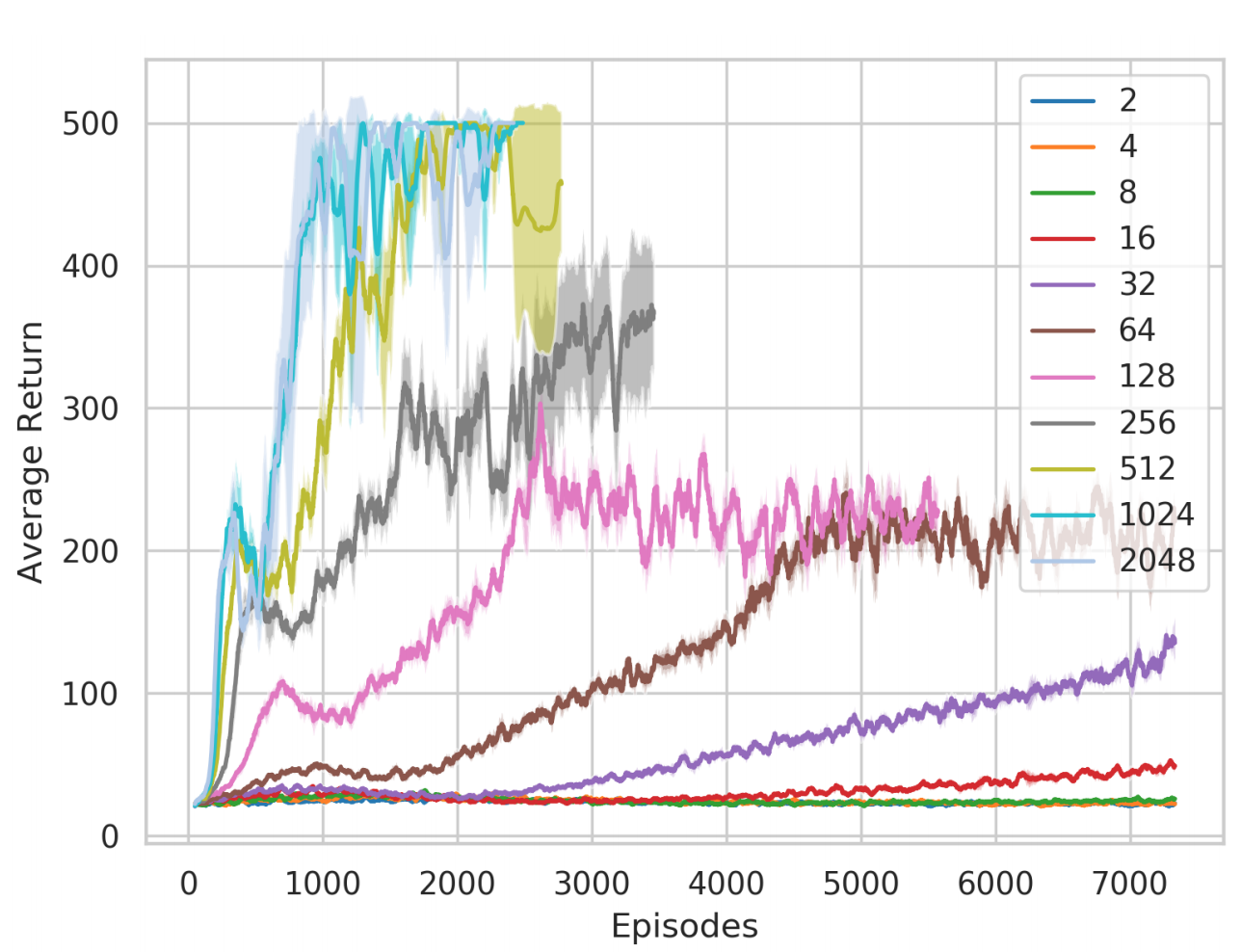In Support of Over-Parametrization in deep RL There is significant recent evidence in supervised learning that, in the over-parametrized setting, wider networks achieve better test error. We experiment on four OpenAI Gym tasks and provide evidence that overparametrization is also beneficial in deep RL.
Lead: Brady Neal -
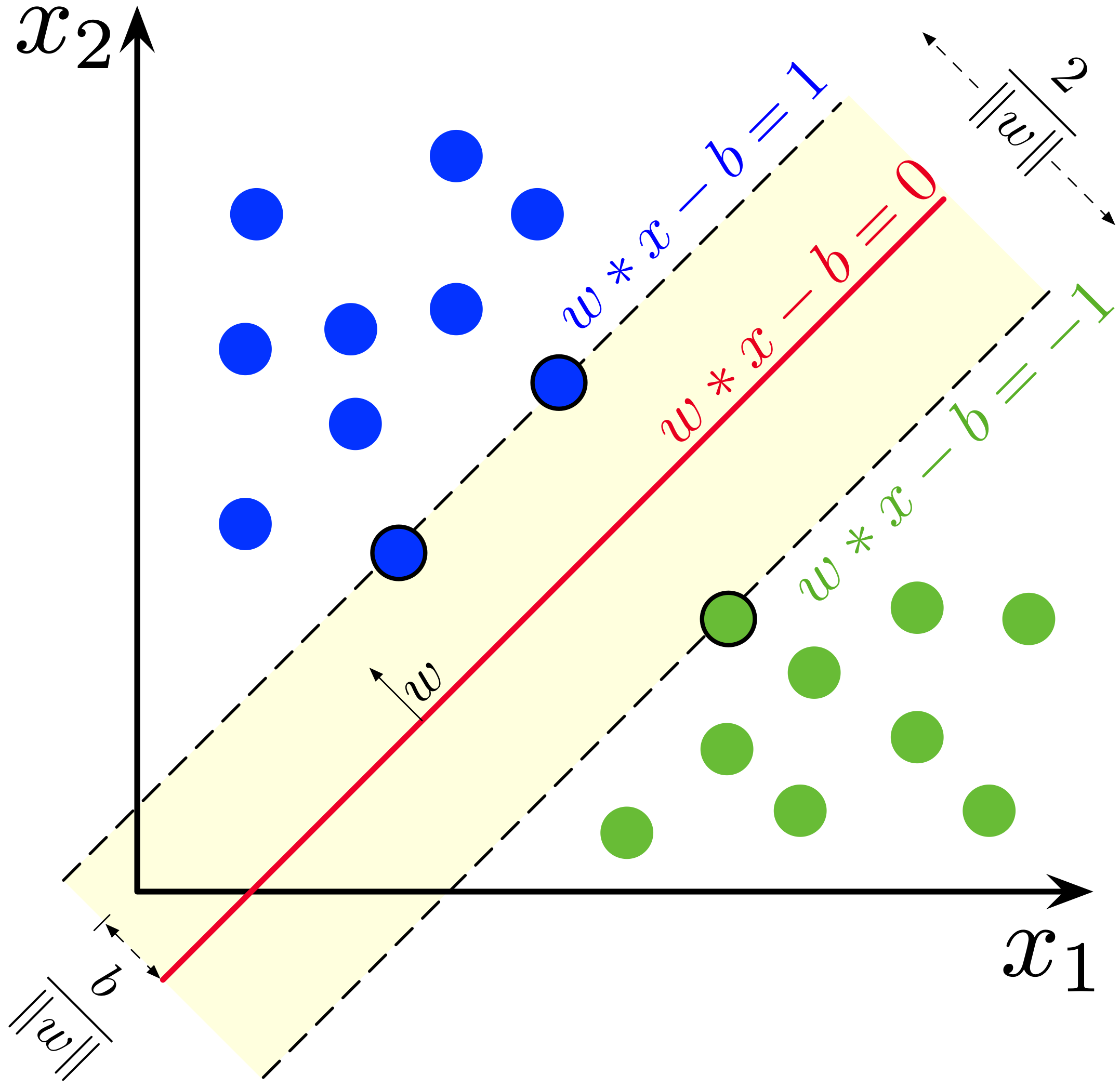Connections between max margin classifiers and gradient penalties Maximum-margin classifiers can be formulated as Integral Probability Metrics (IPMs) or classifiers with some form of gradient norm penalty. This implies a direct link to a class of Generative adversarial networks (GANs) which penalize a gradient norm.
Lead: Alexia Jolicoeur-Martineau, Image source: wikipedia
Differentiable games
-
Consensus Optimization for Smooth Games: Convergence Analysis under Expected Co-coercivity We introduce expected co-coercivity and provide the first last-iterate convergence guarantees of SGDA and SCO for a class of non-monotone stochastic variational inequality problems.
Lead: Nicolas Loizou -
LEAD: Least-Action Dynamics for Min-Max Optimization We leverage tools from physics to introduce LEAD (Least-Action Dynamics), a second-order optimizer for min-max games
Lead: Reyhane Askari, Amartya Mitra -
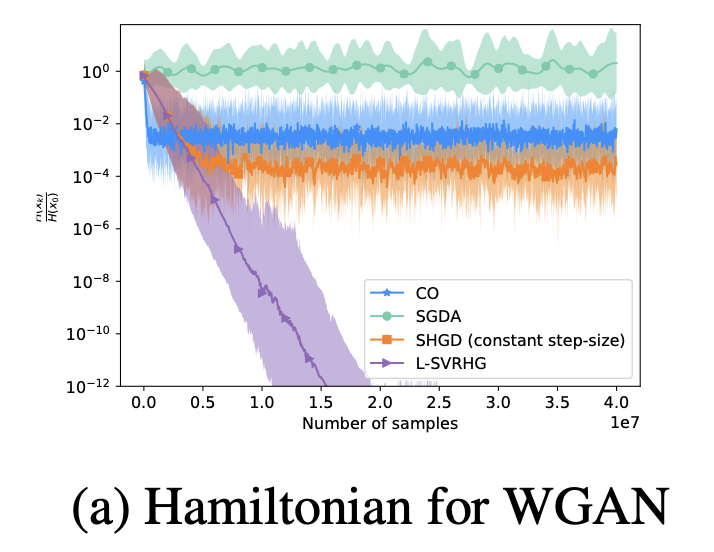Stochastic hamiltonian gradient methods for smooth games We provide the first complete analysis of stochastic Hamiltonian gradient descent with a decreasing step-size, a method successful in training GANs. We also present the first stochastic variance reduced Hamiltonian method.
Lead: Nicolas Loizou -
Accelerating Smooth Games by Manipulating Spectral Shapes We use matrix iteration theory to characterize acceleration in smooth games. The spectral shape of a family of games is the set containing all eigenvalues of the Jacobians of standard gradient dynamics in the family.
Lead: Waiss Azizian -
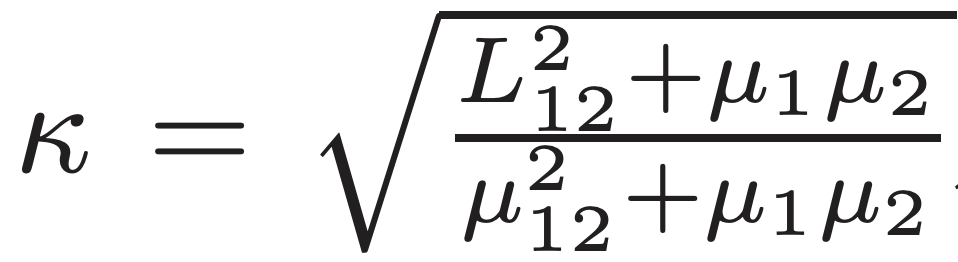Linear Lower Bounds and Conditioning of Differentiable Games We approach the question of fundamental iteration complexity for smooth, differentiable games by providing lower bounds to complement the linear (i.e. geometric) upper bounds observed in the literature on a wide class of problems.
Lead: Adam Ibrahim -
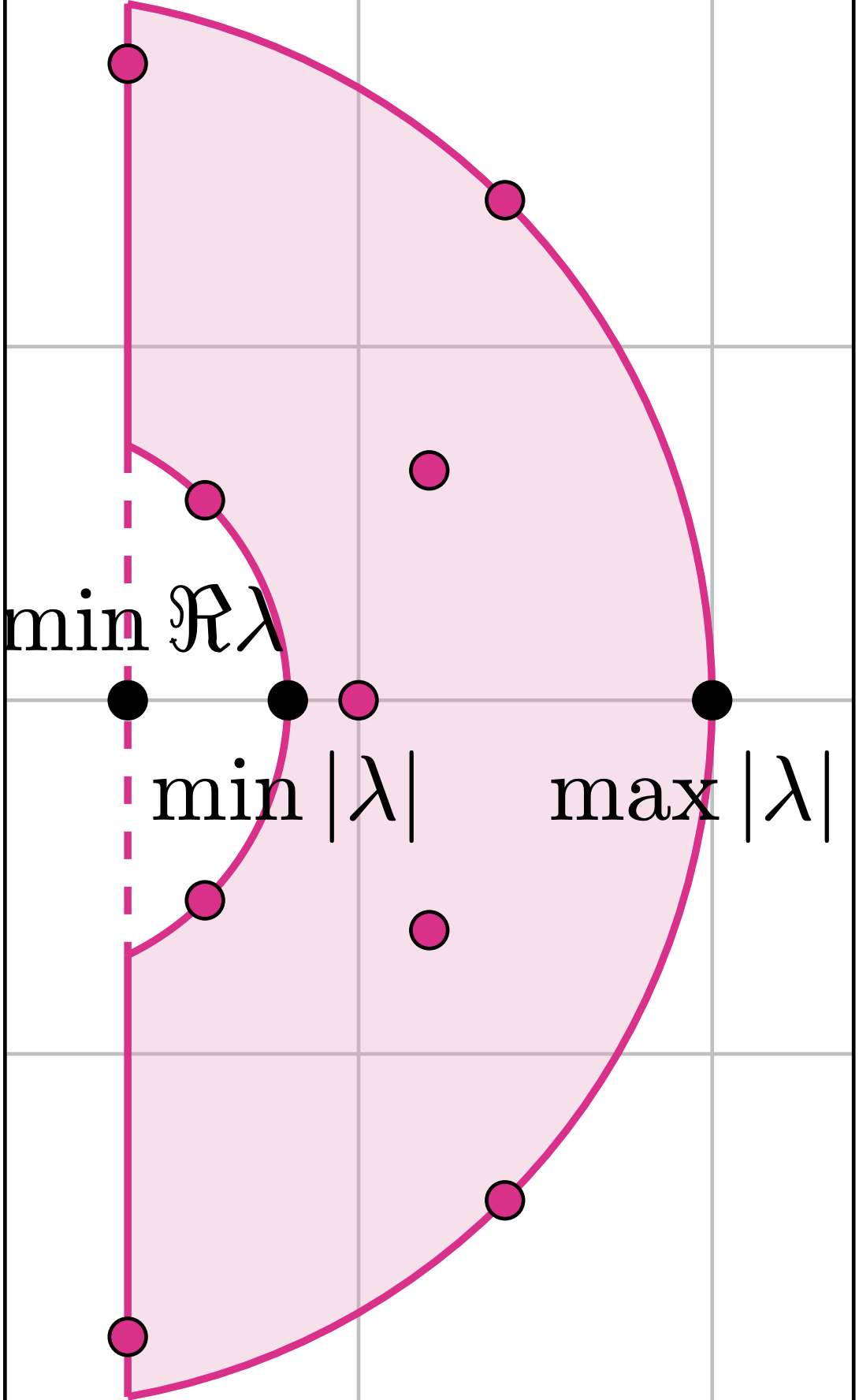A Unified Analysis of gradient methods for a Whole Spectrum of Games We provide new analyses of the extragradient's local and global convergence properties and tighter rates for optimistic gradient and consensus optimization. Unlike in convex minimization, EG may be much faster than gradient descent.
Lead: Waiss Azizian -
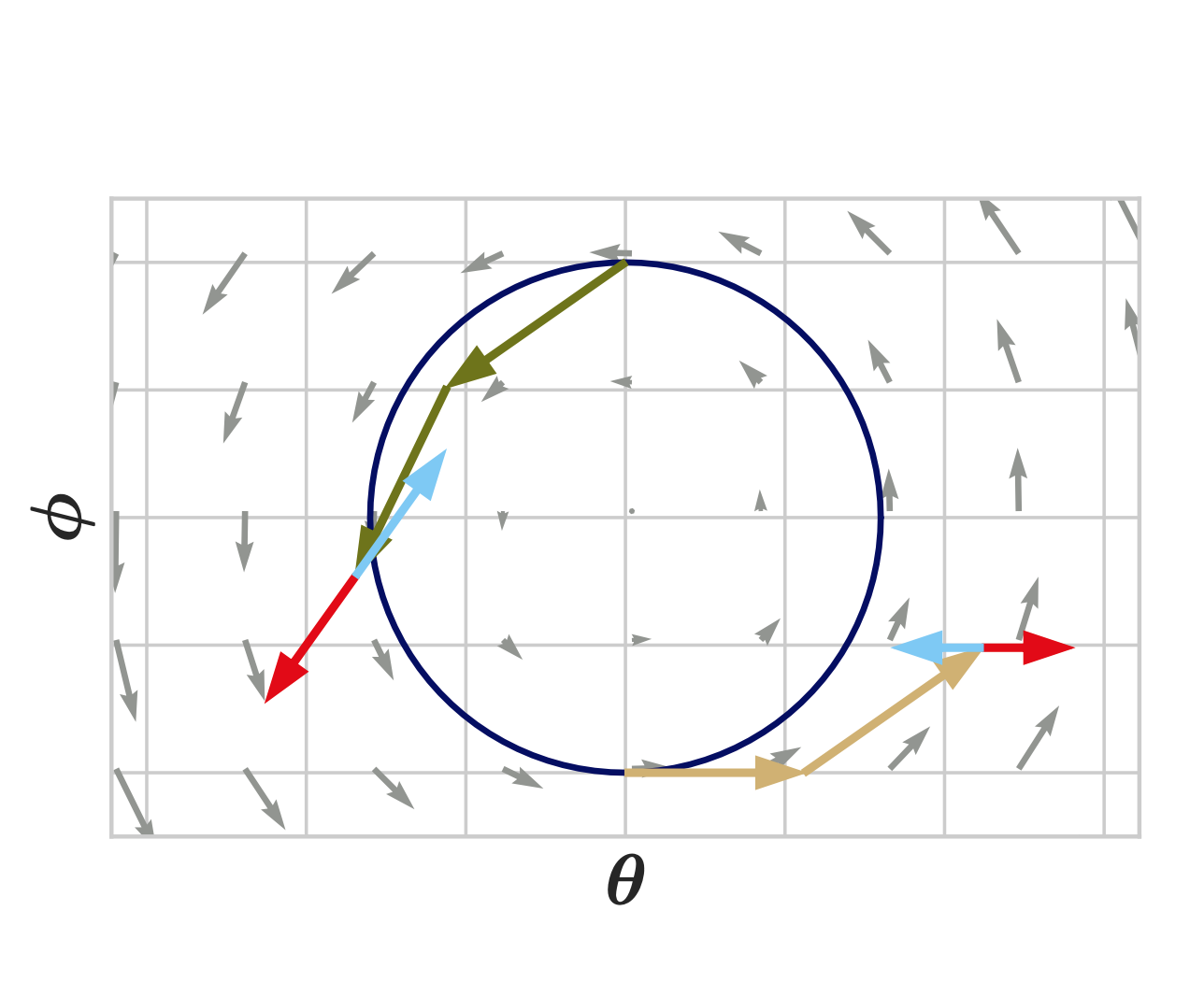Negative Momentum for Improved Game Dynamics Alternating updates are more stable than simultaneous updates on simple games. A negative momentum term achieves convergence in a difficult toy adversarial problem, but also on the notoriously difficult to train saturating GANs
Lead: Gauthier Gidel, Reyhane Askari-Hemmat
Generative models
-
Gotta Go Fast When Generating Data with Score-Based Models We borrow tools and ideas from stochastic differential equation literature to devise a more efficient solver for score-based diffusion generative models. Our approach generates data 2 to 10 times faster than EM while achieving better or equal sample quality.
Lead: Alexia Jolicoeur-Martineau -
Adversarial score matching and sampling for image generation We dig into recently proposed deep generative methods based on denoising score mathing and annealed Langevin Sampling (DSM-ALS). We identify two weaknesses in existing methodology and address them to provide state-of-the-art generative performance.
Lead: Alexia Jolicoeur-Martineau -
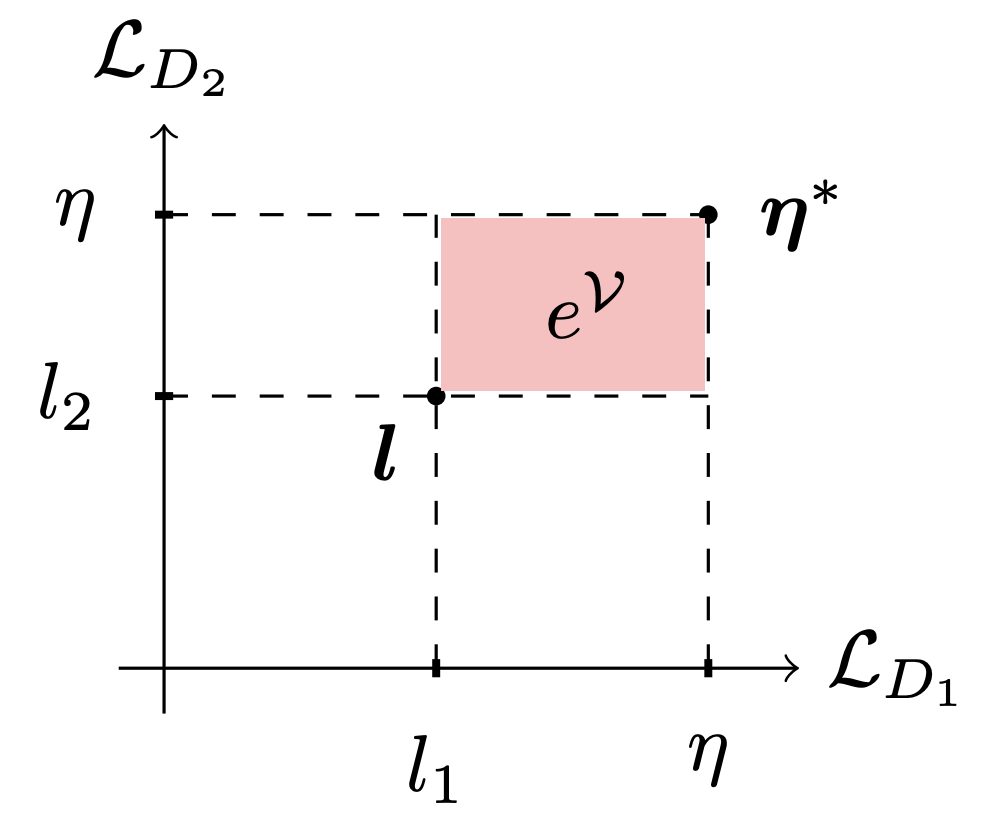Multi-objective training of GANs with multiple discriminators We study GANs with multiple discriminators by framing them as a multi-objective optimization problem. Our results indicate that hypervolume maximization presents a better compromise between sample quality and computational cost than previous methods.
Lead: Isabela Albuquerque, João Monteiro (INRS)
Optimization and numerical analysis
-
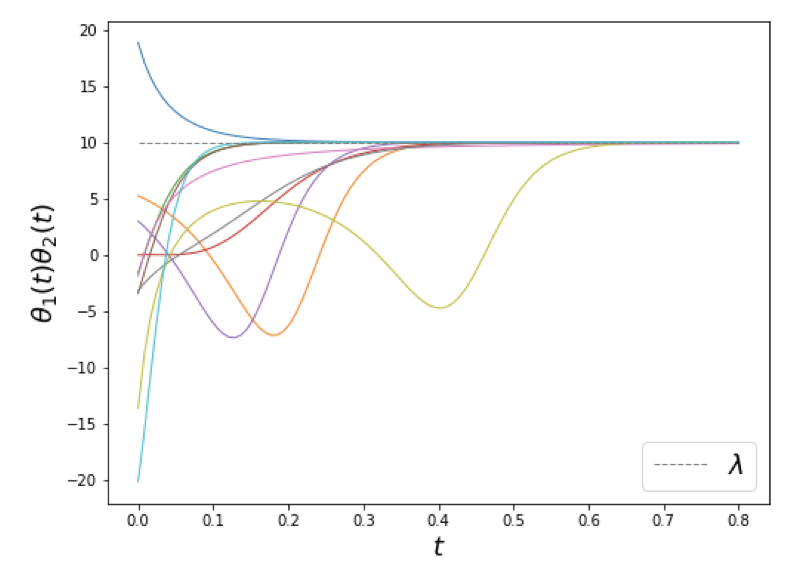Implicit Regularization with Feedback Alignment We analyze feedback alignment and study incremental learning phenomena for linear networks. Interestingly, certain initializations imply that negligible components are learned before the principal ones; a phenomenon we classify as implicit anti-regularization.
Lead: Manuela Girotti -
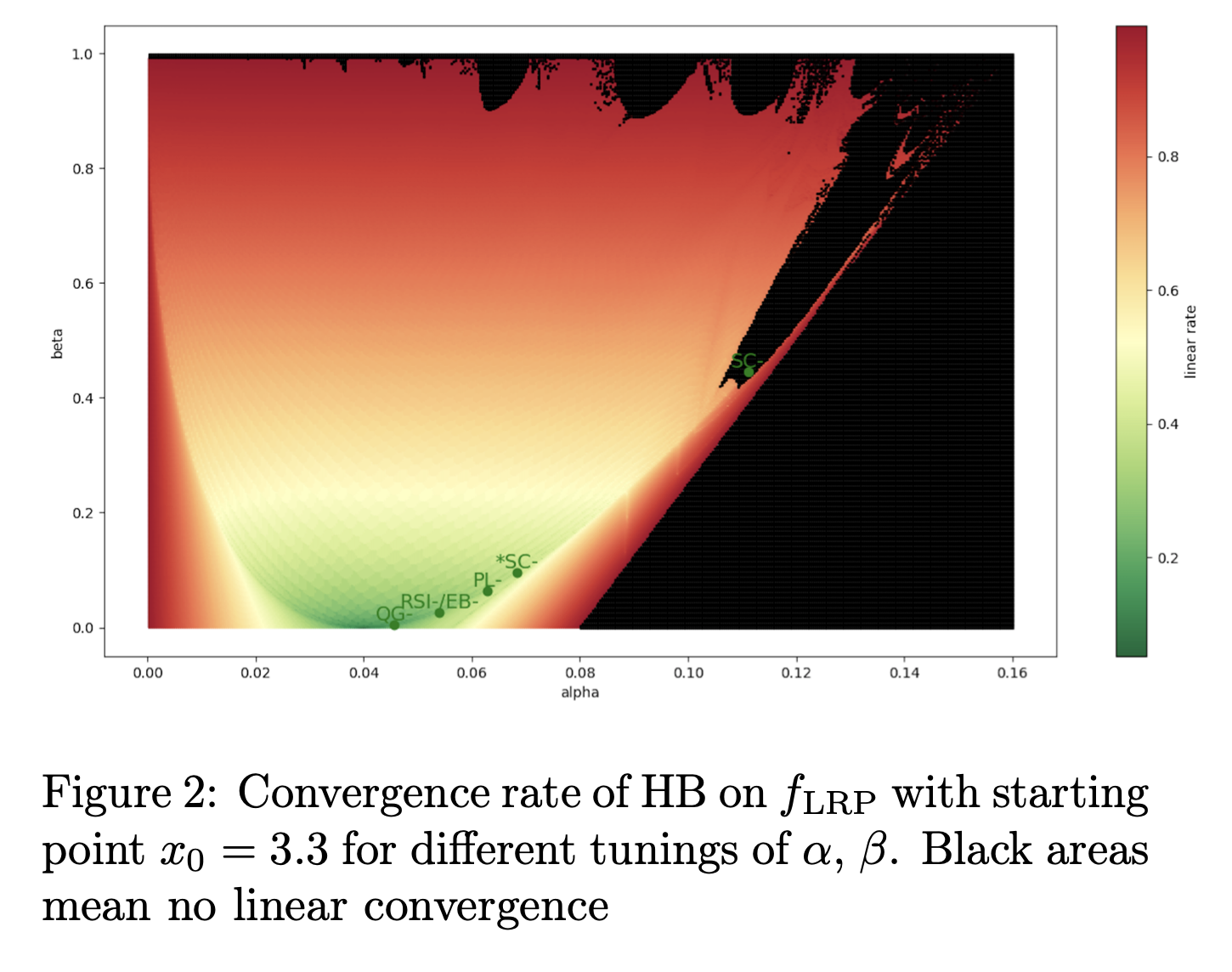A Study of Condition Numbers for First-Order Optimization Condition numbers are not continuous!! (seriously it wreaks havoc with tuning) We perform a comprehensive study of alternative metrics which we prove to be continuous. Finally we discuss how our work impacts the theoretical understanding of FOA and their performances.
Lead: Charles Guille-Escuret, Baptiste Goujaud -
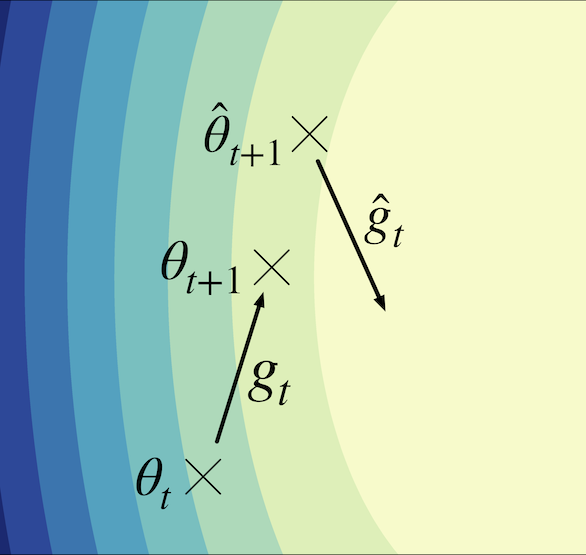Reducing variance in online optimization by transporting past gradients Implicit gradient transport turns past gradients into gradients evaluated at the current iterate. It reduces the variance in online optimization and can be used as a drop-in replacement for the gradient estimate in a number of well-understood methods such as heavy ball or Adam.
Lead: Sebastien Arnold -
YellowFin: Self-tuning optimization for deep learning Simple insights on the momentum update yield an very efficient parameter-free algorithm that performs well across networks and datasets without the need to tune any parameters.
Lead: Jian Zhang -
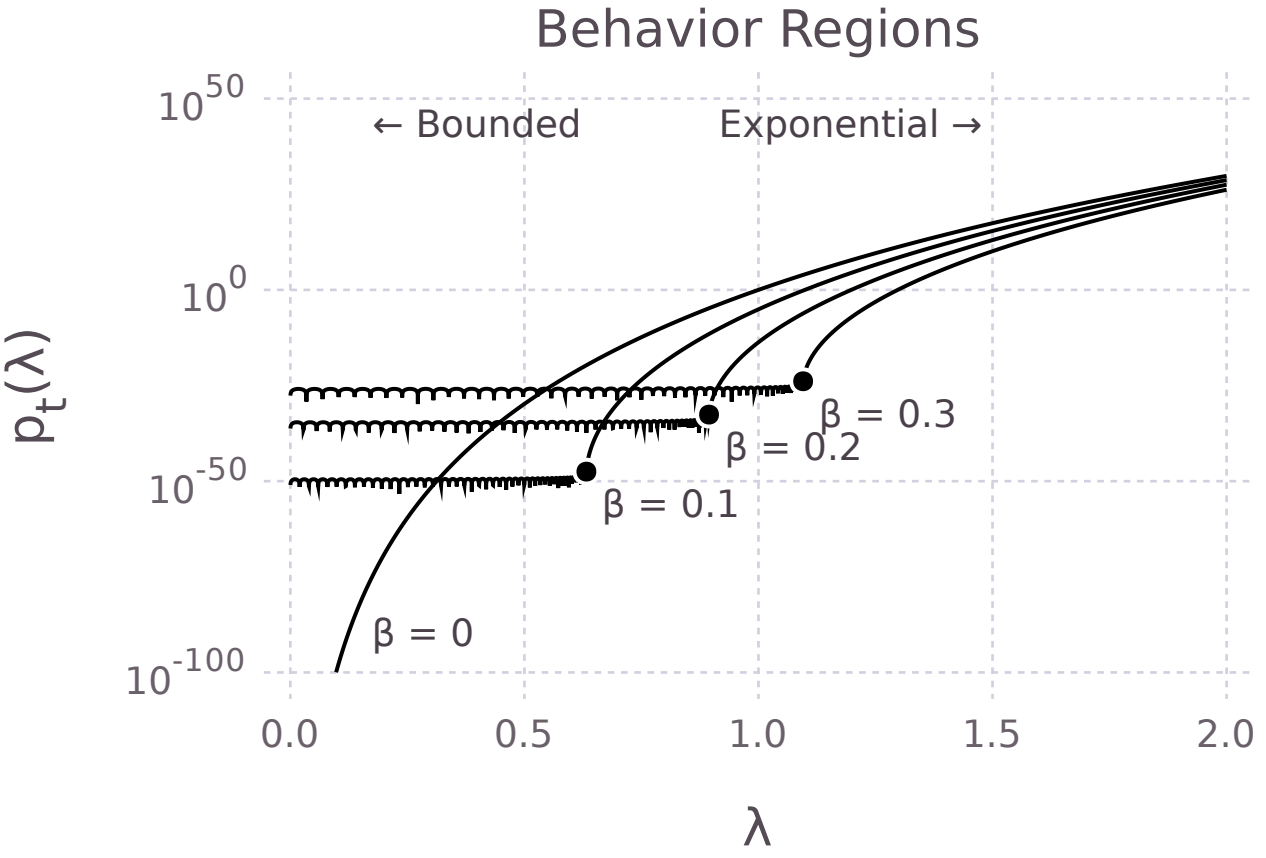Accelerated stochastic power iteration Exciting recent results on how adding a momentum term to the power iteration yields a numerically stabe, accelerated method.
Lead: Peng Xu -
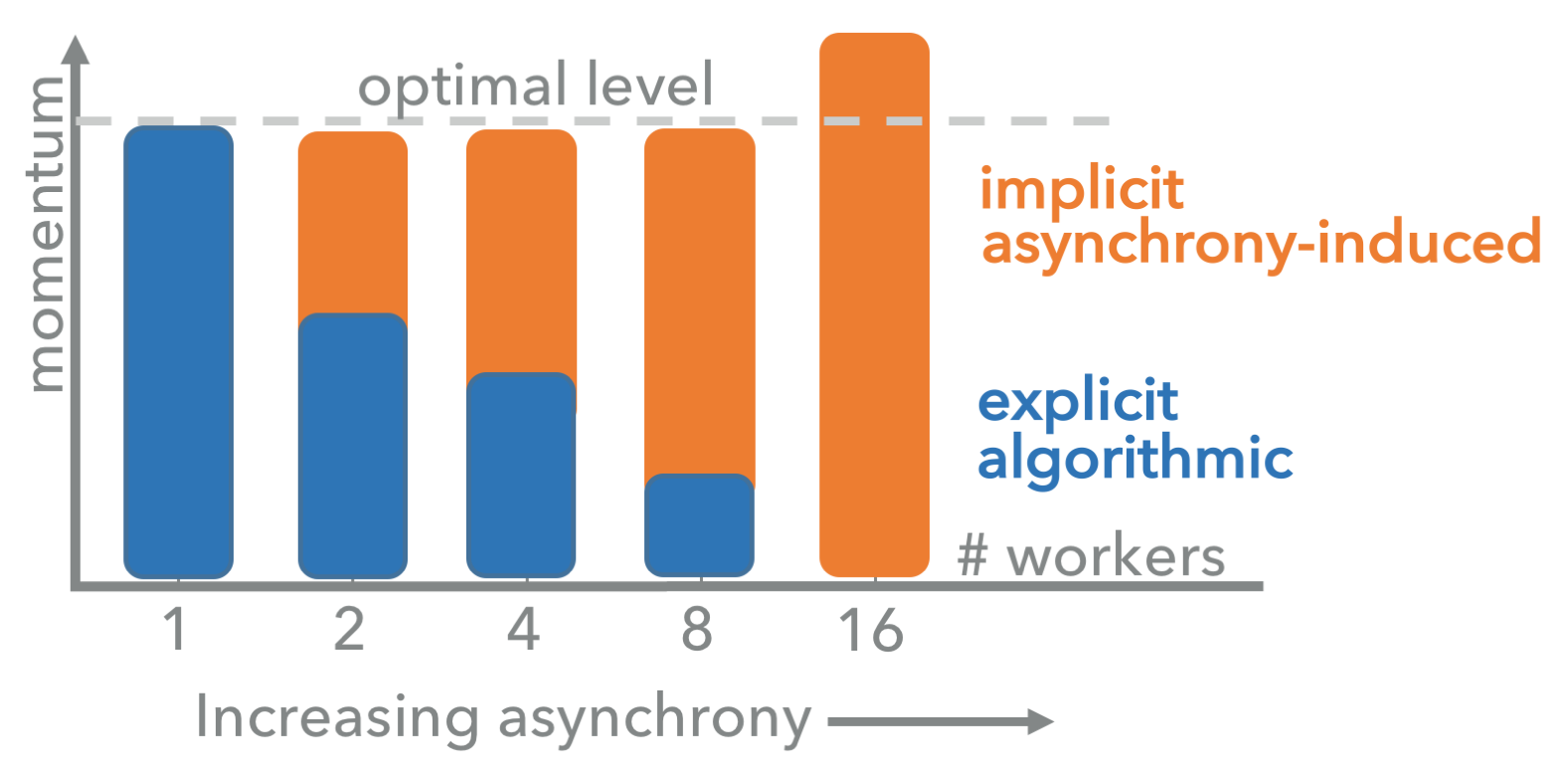Asynchrony begets momentum When training large-scale systems asynchronously, you get a momentum surprise. We prove that system dynamics "bleed" into the algorithm introducing a momentum term even when the algorithm uses none. This theoretical result has very significant implications on large-scale optimization systems. -
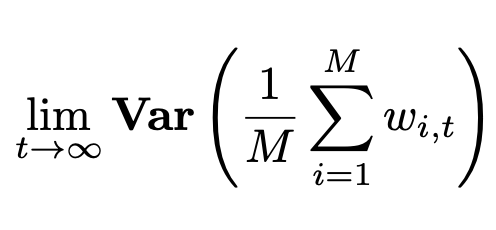Parallel SGD: When does averaging help? Averaging as a variance-reducing mechanism. For convex objectives, we show the benefit of frequent averaging depends on the gradient variance envelope. For non-convex objectives, we illustrate that this benefit depends on the presence of multiple optimal points.
Lead: Jian Zhang -
Memory Limited, Streaming PCA An algorithm that uses O(kp) memory and is able to compute the k-dimensional spike with quasi-optimal, O(plogp), sample-complexity -- the first algorithm of its kind.
Deep learning and applications
-
State-Reification Networks We model the distribution of hidden states over the training data and then project test hidden states on this distribution. This method helps neural nets generalize better, and overcome the challenge of achieving robust generalization with adversarial training
Lead: Alex Lamb; oral presentation at ICML 2019 -
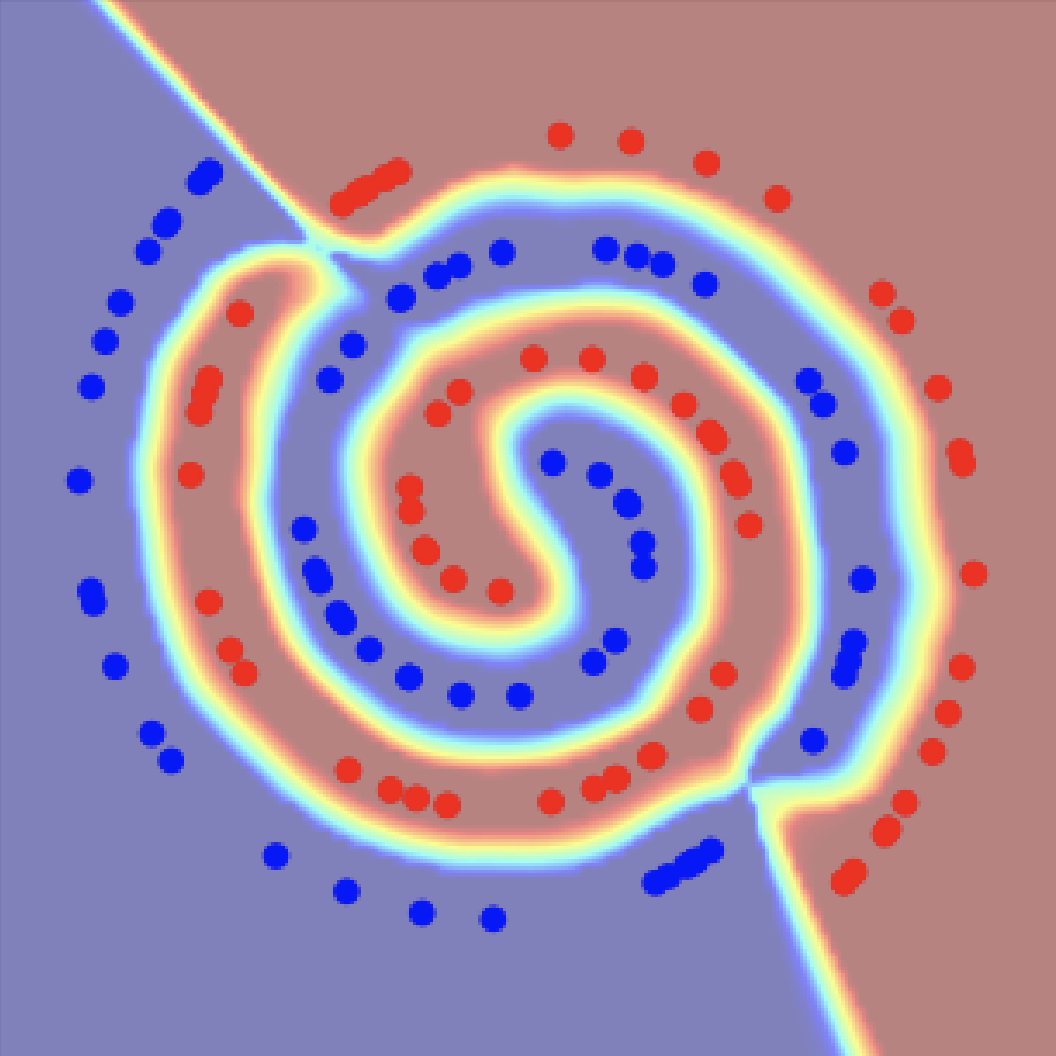Manifold Mixup: Better Representations by Interpolating Hidden States Simple regularizer that encourages neural networks to predict less confidently on interpolations of hidden representations. Manifold mixup improves strong baselines in supervised learning, robustness to single-step adversarial attacks, and test log-likelihood.
Lead: Vikas Verma, Alex Lamb -
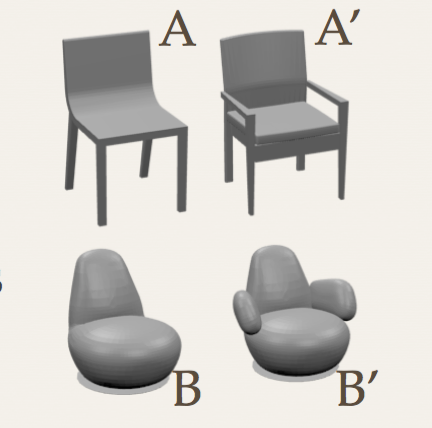Deep representations and Adversarial Generation of 3D Point Clouds The first AutoEncoder design suited to 3D point cloud data beats state of the art in reconstruction accuracy. GANs trainined in the AE's latent space generate realistic objects from every-day classes.
Lead: Panos Achlioptas
MCMC methods
Large-scale systems
-
MLSys: The New Frontier of Machine Learning Systems We propose to foster a new systems machine learning research community at the intersection of the traditional systems and ML communities, focused on topics such as
Whitepaper -
Deep Learning at 15 Petaflops 15-PetaFLOP Deep Learning system for solving scientific pattern classification problems on contemporary HPC architectures. We scale to 10,000 nodes by implementing a hybrid synchronous/asynchronous system and applying careful optimization of hyperparameters.
Collaboration with NERSC at Lawrence Berkeley Labs and Intel. -
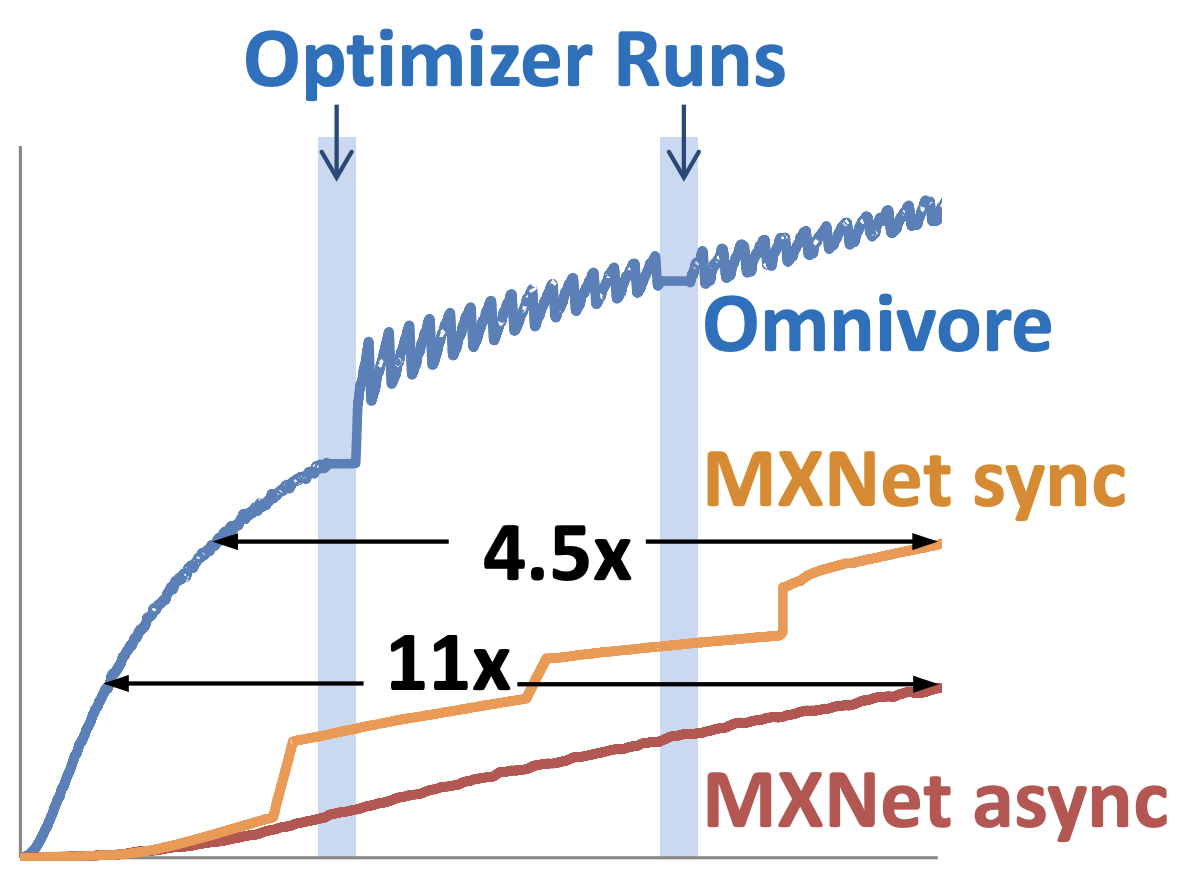Omnivore: Optimizer for multi-device deep learning A high performance system prototype combining a number of much needed algorithmic and software optmimizations. Importantly, we identify the degree of asynchronous parallelization as a key factor affecting both hardware and statistical efficiency.
Lead: Stefan Hadjis -
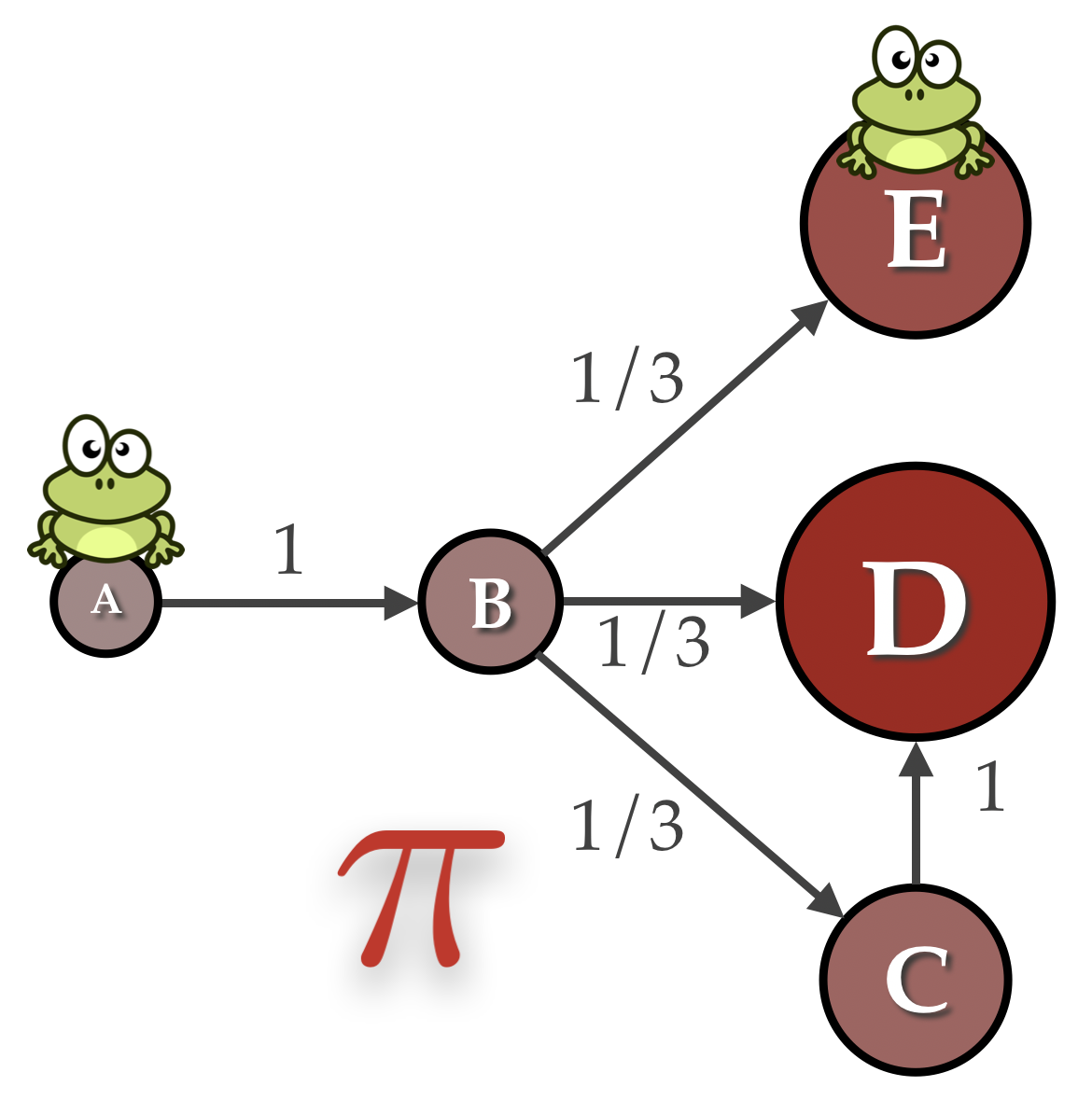FrogWild! - Fast PageRank approximations on Graph Engines Using random walks and a simple modification of the GraphLab egine, we manage to get a 7x improvement compared to the state of the art. -
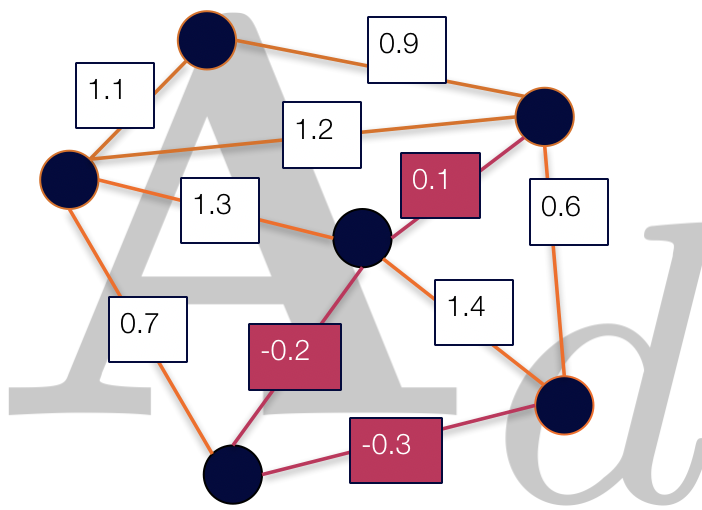Finding Dense Subgraphs via Low-Rank Bilinear Optimization Our method searches a low-dimensional space for provably dense subgraphs of graphs with billions of edges. We provide data dependent guarantees on the quality of the solution that depend on the graph spectrum.
Lead: Dimitris Papailiopoulos